A Certifiably Correct Algorithm for Synchronization over the Special Euclidean Group
Abstract
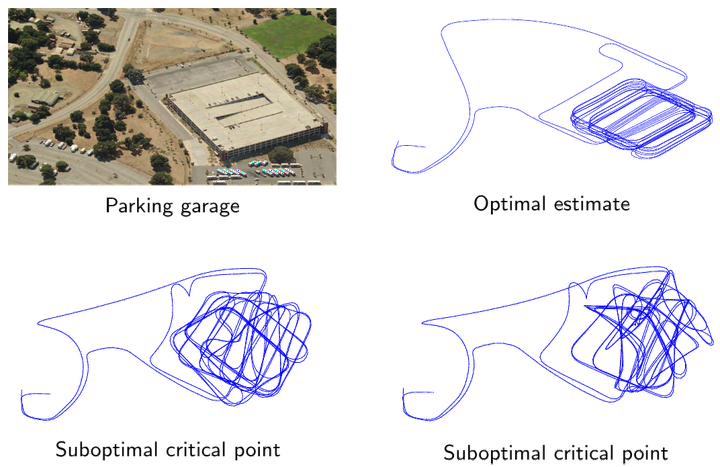
Many important geometric perception tasks require synchronization over the special Euclidean group: estimate a set of unknown poses (positions and orientations in 2D or 3D space) from a collection of noisy relative measurements between them. Examples of this class include the foundational problems of pose-graph SLAM (in robotics), camera motion estimation (in computer vision), and sensor network localization (in distributed sensing), among others. This inference problem is typically formulated as a nonconvex maximum likelihood estimation that is computationally hard to solve in general. In practice, this hardness manifests in the form of many significantly suboptimal local minima that can entrap standard local optimization methods. To address this pitfall, in this work we propose a new approach to special Euclidean synchronization based upon convex relaxation rather than local search. We develop a (convex) semidefinite relaxation of the estimation problem whose minimizer provides an exact (globally optimal) maximum likelihood estimate so long as the noise on the available measurements is not too large; furthermore, whenever this holds, it is possible to verify this fact a posteriori, thereby certifying the optimality of the recovered estimate. In practice, our algorithm (SE-Sync) is capable of recovering certifiably globally optimal solutions when the available measurements are corrupted by noise up to an order of magnitude greater than that typically encountered in robotics and computer vision applications, and does so more than an order of magnitude faster than the Gauss-Newton-based approach that forms the basis of current state-of-the-art techniques.
Best Paper Award